The prototype for the first big piece of BEPUphysics v2.0.0 is pretty much done: a tree.
This tree will (eventually) replace all the existing trees in BEPUphysics and act as the foundation of the new broad phase.
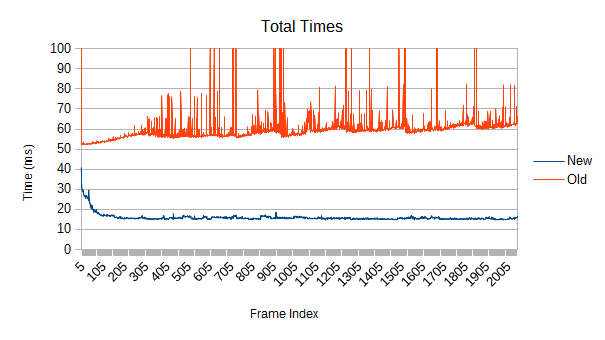
So how does the current prototype compare with v1.4.0's broad phase?
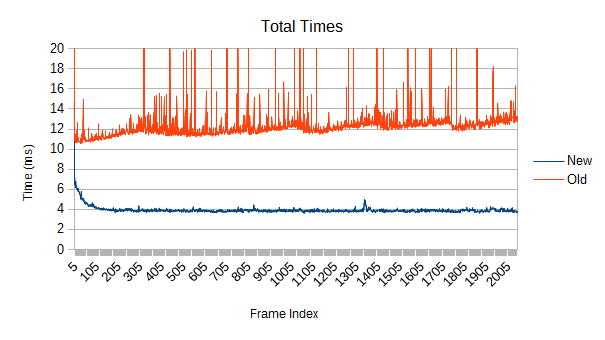
It's a lot faster.
The measured 'realistic' test scene includes 65536 randomly positioned cubic leaves ranging from 1 to 100 units across, with leaf size given by 1 + 99 * X^10, where X is a uniform random value from 0 to 1. In other words, there are lots of smaller objects and a few big objects, and the average size is 10 units. All leaves are moving in random directions with speeds given by 10 * X^10, where X is a uniform random value from 0 to 1, and they bounce off the predefined world bounds (a large cube) so that they stay in the same volume. The number of overlaps ranges between 65600 and 66300.
Both simulations are multithreaded with 8 threads on a 3770K@4.5ghz. Notably, the benchmarking environment was not totally clean. The small spikes visible in the new implementation do not persist between runs and are just the other programs occasionally interfering.
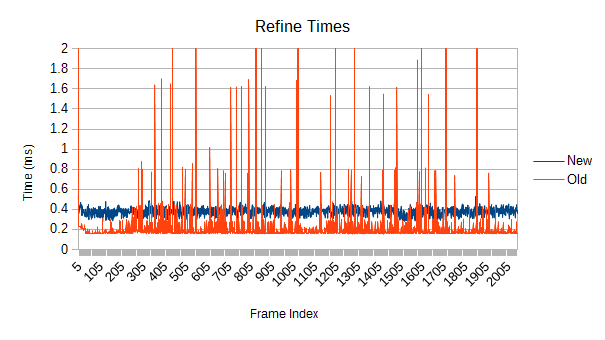
So, the first obvious thing you might notice is that the old version spikes like crazy. Those spikes were a driving force behind this whole rewrite. What's causing them, and how bad can they get?
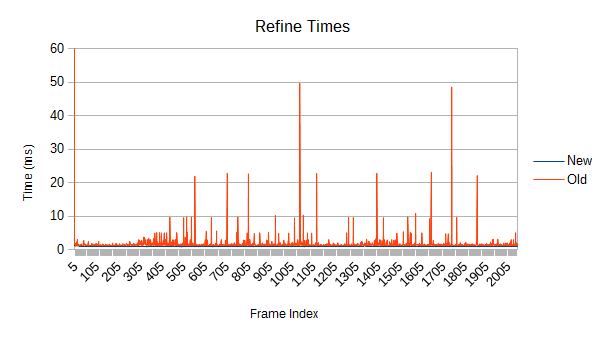
The answers are refinement and really bad. Each one of those spikes represents a reconstruction of part of the tree which has expanded beyond its optimal size. Those reconstructions aren't cheap, and more importantly, they are unbounded. If a reconstruction starts near the root, it may force a reconstruction of large fractions of the tree. If you're really unlucky, it will be so close to the root that the main thread has to do it. In the worst case, the root itself might get reconstructed- see that spike on frame 0? The graph is actually cut off; it took 108ms. While a full root reconstruction usually only happens on the first frame, the other reconstructions are clearly bad enough. These are multi-frame spikes that a user can definitely notice if they're paying attention. Imagine how that would feel in VR.
To be fair to the old broad phase, this test is a lot more painful than most simulations. The continuous divergent motion nearly maximizes the amount of reconstruction required.
But there's something else going on, and it might be even worse. Notice that slow upward slope in the first graph? The new version doesn't have it at all, so it's not a property of the scene itself. What does the tree quality look like?
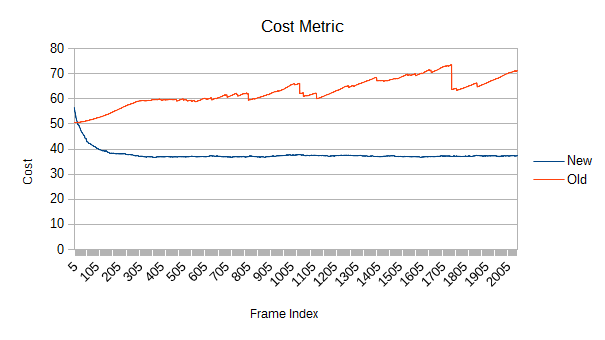
This graph represents the computed cost of the tree. If you've heard of surface area heuristic tree builders in raytracing, this is basically the same thing except the minimized metric is volume instead of surface area. (Volume queries and self collision tests have probability of overlap proportional to volume, ray-AABB intersection probability is proportional to surface area. They usually produce pretty similar trees, though.)
The new tree starts with poor quality since the tree was built using incremental insertion, but the new refinement process quickly reduces cost. It gets to around 37.2, compared to a full sweep rebuild of around 31.9.
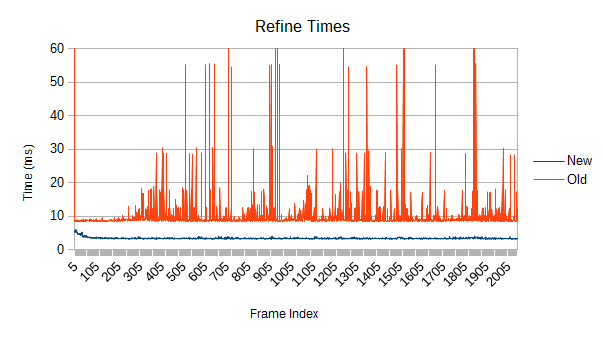
The old tree starts out better since the first frame's root reconstruction does a full median split build. But what happens afterward? That doesn't look good. What happens if tree churns faster? How about a bunch of objects moving 10-100 instead of 0-10 units per second, with the same distribution?
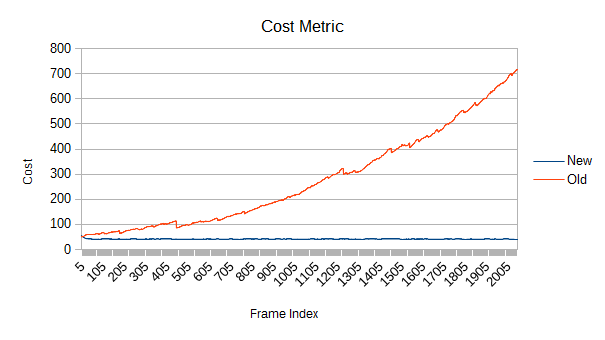
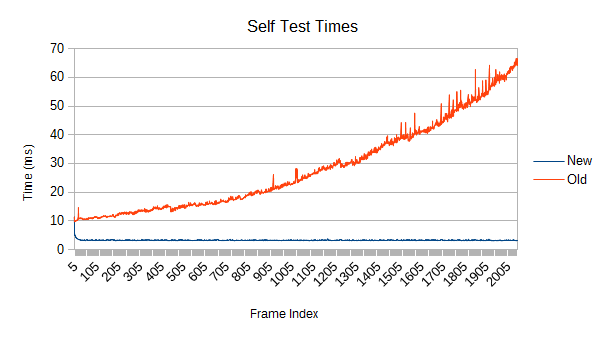

Uh oh. The cost increases pretty quickly, and the self test cost rises in step. By the end, the new version is well over 10 times as fast. As you might expect, faster leaf speeds are even worse. I neglected to fully benchmark that since a cost metric 10000 times higher than it should be slows things down a little.
What's happening?
The old tree reconstructs nodes when their volume goes above a certain threshold. After the reconstruction, a new threshold is computed based on the result of the reconstruction. Unfortunately, that new threshold lets the tree degrade further next time around. Eventually, the threshold ratchets high enough that very few meaningful refinements occur. Note in the graph that the big refinement time spikes are mostly gone after frame 1000. If enough objects are moving chaotically for long periods of time, this problem could show up in a real game.
This poses a particularly large problem for long-running simulations like those on a persistent game server. The good news is that the new version has no such problem, the bad news is that there is no good workaround for the old version. For now, if you run into this problem, try periodically calling DynamicHierarchy.ForceRebuild (or look for the internal ForceRevalidation in older versions). As the name implies, it will reset the tree quality but at a hefty price. Expect to drop multiple frames.
(This failure is blindingly obvious in hindsight, and I don't know how I missed it when designing it, benchmarking it, or using it. I'm also surprised no one's reported it to my knowledge. Oops!)
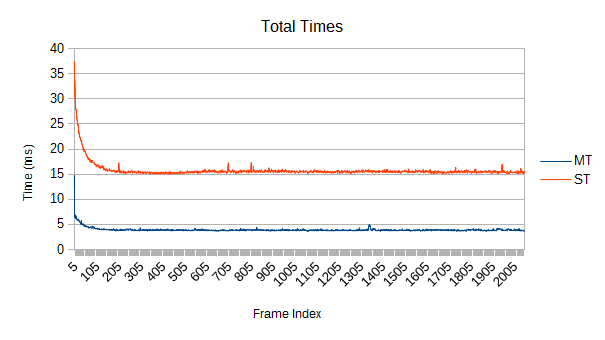
So, how about if nothing is moving?
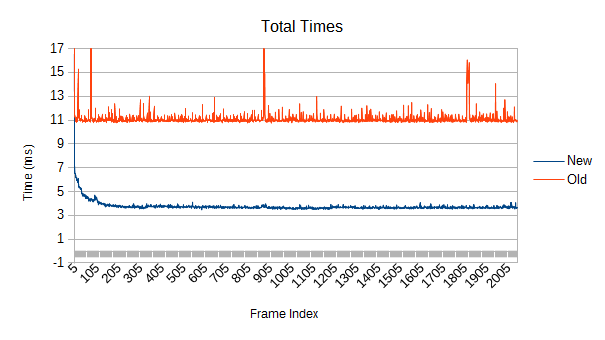
The old version manages to maintain a constant slope, though it still has some nasty spikes. Interestingly, those aren't primarily from refinement, as we'll see in a moment.
This is also a less favorable comparison for the new tree, "only" being 3 times as fast.
Splitting the time contributions helps explain both observations:
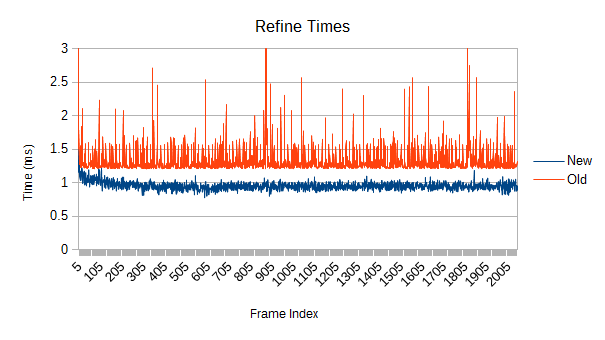
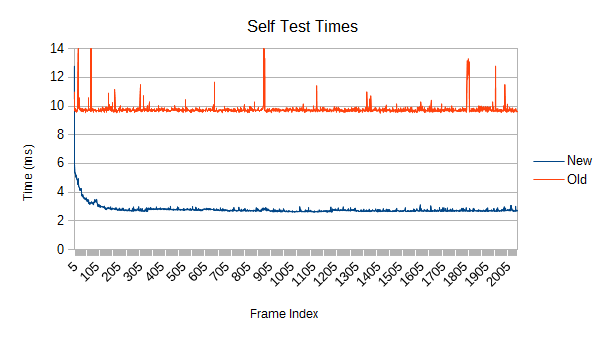
The old version's spikes can't be reconstructions given that everything is totally stationary, and the self test shows them too. I didn't bother fully investigating this, but one possible source is poor load balancing. It uses a fairly blind work collector, making it very easy to end up with one thread overworked. The new version, in contrast, is smarter about selecting subtasks of similar size and also collects more of them.
So why is the new refinement only a little bit faster if the self test is 3.5 times faster? Two reasons. First, the new refinement is never satisfied with doing no work, so in this kind of situation it does a bit too much. Second, I just haven't spent much time optimizing the refinement blocks for low work situations like this. These blocks are fairly large compared to the needs of a totally stationary tree, so very few of them need to be dispatched. In this case, there were only 2. The other threads sit idle during that particular subphase. In other words, the new tree is currently tuned for harder workloads.
Now, keeping leaves stationary, what happens when the density of leaves is varied? First, a sparse distribution with 8 times the volume (and so about one eighth the overlaps):
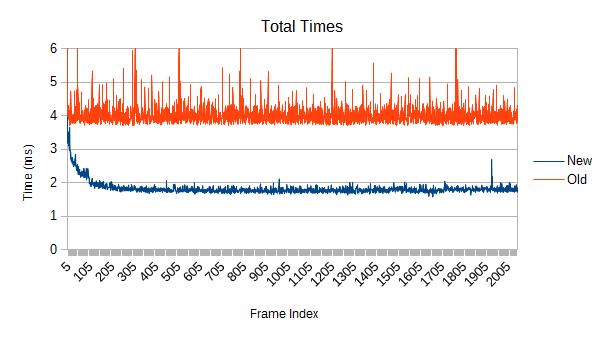
A bit over twice as fast. A little disappointing, but this is another one of those 'easy' cases where the new refinement implementation doesn't really adapt to very small workloads, providing marginal speedups.
How about the reverse? 64 times more dense than the above, with almost 500000 overlaps. With about 8 overlaps per leaf, this is roughly the density of a loose pile.
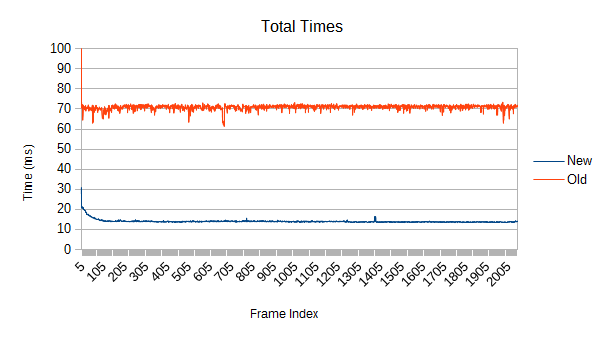
Despite the fact that the refinement suffers from the same 'easy simulation' issue, the massive improvement in test times brings the total speedup to over 5 times faster. The new tree's refinement takes less than a millisecond on both the sparse and dense cases, but the dense case stresses the self test vastly more. And the old tree is nowhere near as fast at collision tests.
Next up: while maintaining the same medium density of leaves (about one overlap per leaf), vary the number. Leaves are moving at the usual 0-10 speed again for these tests. First, a mere 16384 leaves instead of 65536:
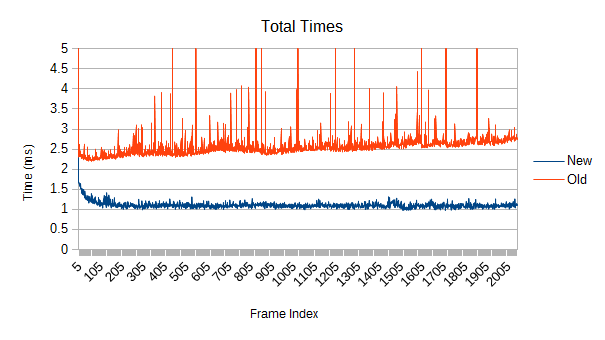
Only about 2.5 times faster near the end. The split timings are interesting, though:
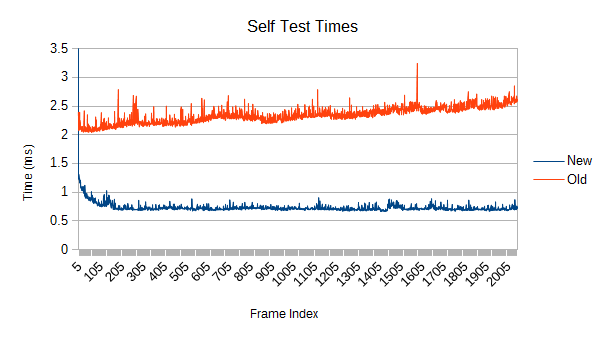
The self test marches along at around 3.5 times as fast near the end, but the refinement is actually slower... if you ignore the enormous spikes of the old version. Once again, there's just not enough work to do and the work chunks are too big at the moment. 400 microseconds pretty okay, though.
How about a very high leaf count, say, 262144 leaves?
Around 4 times as fast. Refinement has enough to chomp on.
Refinement alone hangs around 2.5-2.75 times as fast, which is pretty fancy considering how much more work it's doing. As usual, the self test is super speedy, only occasionally dropping below 4.20 times as fast.
How about multithreaded scaling? I haven't investigated higher core counts yet, but here are the new tree's results for single threaded versus full threads on the 3770K under the original 65536 'realistic' case:
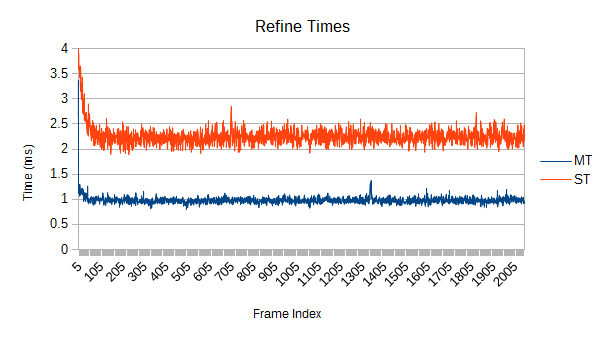
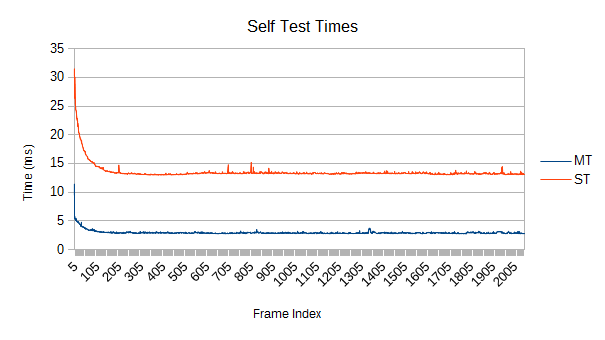
Very close to exactly 4 times as fast total. Self tests float around 4.5 times faster. As described earlier, this kind of 'easy' simulation results in a fairly low scaling in refinement- only about 2.3 times faster. If everything was flying around at higher speeds, refinement would be stressed more and more work would be available.
For completeness, here's the new tree versus the old tree, singlethreaded, in the same simulation:
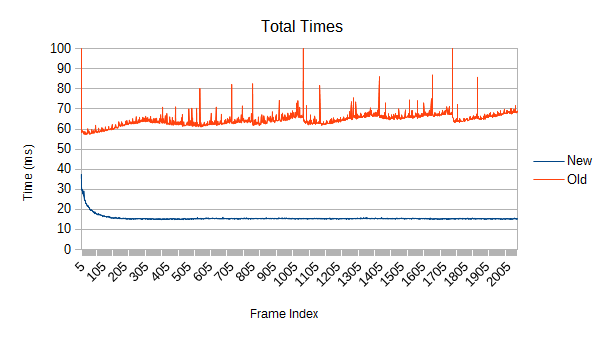
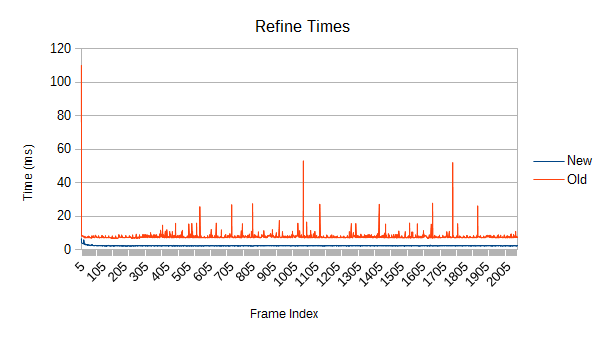
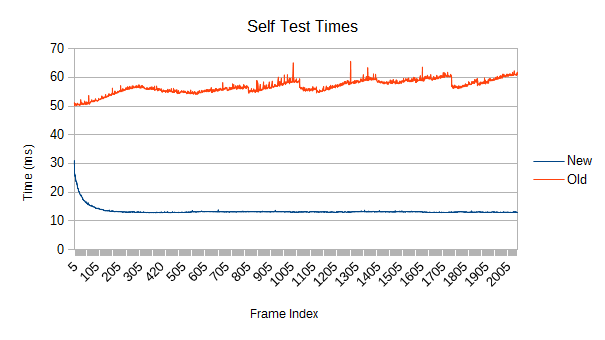
3 times faster refines (ignoring spikes), and about 4.5 faster in general.
How does it work?
The biggest conceptual change is the new refinement phase. It has three subphases:
1) Refit
As objects move, the node bounds must adapt. Rather than doing a full tree reconstruction every frame, the node bounds are recursively updated to contain all their children.
During the refit traversal, two additional pieces of information are collected. First, nodes with a child leaf count below a given threshold are added to 'refinement candidates' set. These candidates are the roots of a bunch of parallel subtrees. Second, the change in volume of every node is computed. The sum of every node's change in volume divided by the root's volume provides the change in the cost metric of the tree for this frame.
2) Binned Refine
A subset of the refinement candidates collected by the refit traversal are selected. The number of selected candidates is based on the refit's computed change in cost; a bigger increase means more refinements. The frame index is used to select different refinement candidates as time progresses, guaranteeing that the whole tree eventually gets touched.
The root always gets added as a refinement target. However, the refinement is bounded. All of these refinements tend to be pretty small. Currently, any individual refinement in a tree with 65536 leaves will collect no more than 768 subtrees, a little over 1%. That's why there are no spikes in performance.
Here's an example of candidates and targets in a tree with 24 leaves:
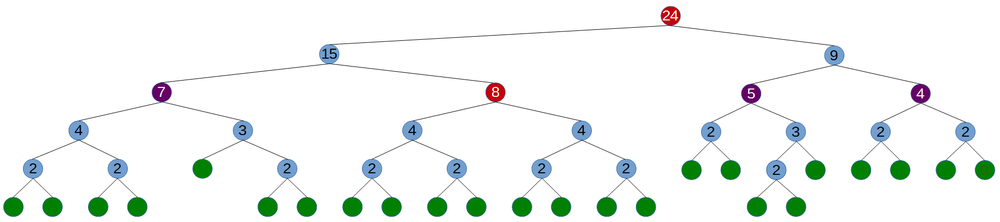
The number within each node is the number of leaves in the children of that node. Green circles are leaf nodes, purple circles are refinement candidates that weren't picked, and red circles are the selected refinement targets. In this case, the maximum number of subtrees for any refinement was chosen as 8.
Since the root has so many potential nodes available, it has options about which nodes to refine. Rather than just diving down the tree a fixed depth, it seeks out the largest nodes by volume. Typically, large nodes tend to be a high leverage place to spend refine time. Consider a leaf node that's moved far enough from its original position that it should be in a far part of the tree. Its parents will tend to have very large bounds, and refinement will see that.
For multithreading, refinement targets are marked (only the refinement treelet root, though- no need to mark every involved node). Refinement node collection will avoid collecting nodes beyond any marked node, allowing refinements to proceed in parallel.
The actual process applied to each refinement target is just a straightforward binned builder that operates on the collected nodes. (For more about binned builders, look up "On fast Construction of SAH-based Bounding Volume Hierarchies" by Ingo Wald.)
3) Cache Optimize
The old tree allocated nodes as reference types and left them scattered through memory. Traversing the tree was essentially a series of guaranteed cache misses. This is not ideal.
The new tree is just a single contiguous array. While adding/removing elements and binned refinements can scramble the memory order relative to tree traversal order, it's possible to cheaply walk through parts of the tree and shuffle nodes around so that they're in the correct relative positions. A good result only requires optimizing a fraction of the tree; 3% to 5% works quite well when things aren't moving crazy fast. The fraction of cache optimized nodes scales with refit-computed cost change as well, so it compensates for the extra scrambling effects of refinement. In most cases, the tree will sit at 80-95% of cache optimal. (Trees with only a few nodes, say less than 4096, will tend to have a harder time keeping up right now, but they take microseconds anyway.)
Cache optimization can double performance all by itself, so it's one of the most important improvements.
As for the self test phase that comes after refinement, it's pretty much identical to the old version in concept. It's just made vastly faster by a superior node memory layout, cache friendliness, greater attention to tiny bits, and no virtual calls.
Interestingly, SIMD isn't a huge part of the speedup. It's used here and there (mainly refit), but not to its full potential. The self test in particular, despite being the dominant cost, doesn't use SIMD at all.
Future work
1) Solving the refinement scaling issue for 'easy' simulations would be nice.
2) SIMD is a big potential area for improvement. As mentioned, this tree is mostly scalar in nature. At best, refit gets decent use of 3-wide operations. My attempts at creating fully vectorized variants tended to do significantly better than the old one, but they incurred too much overhead in many phases and couldn't beat the mostly scalar new version. I'll probably fiddle with it some more when a few more SIMD instructions are exposed, like shuffles; it should be possible to get at least another 1.5 to 2 times speedup.
3) Refinement currently does some unnecessary work on all the non-root treelets. They actually use the same sort of priority queue selection, even though they are guaranteed to eat the whole subtree by the refinement candidate collection threshold. Further, it should be possible to improve the node collection within refinement by taking into account the change in subtree volume on a per-node level. The root refinement would seek out high entropy parts of the tree. Some early testing implied this would help, but I removed it due to memory layout conflicts.
4) I suspect there are some other good options for the choice of refinement algorithm. I already briefly tried agglomerative and sweep refiners (which were too slow relative to their quality advantage), but I didn't get around to trying things like brute forcing small treelet optimization (something like "Fast Parallel Construction of High-Quality Bounding Volume Hierarchies"). I might revisit this when setting up the systems of the next point.
5) It should be possible to improve the cache optimization distribution. Right now, the multithreaded version is forced into a suboptimal optimization order and suffers from overhead introduced by lots of atomic operations. Some experiments with linking cache optimization to the subtrees being refined showed promise. It converged with little effort, but it couldn't handle the scrambling effect of root refinement. I think this is solvable, maybe in combination with #4.
6) Most importantly, all of the above assumes a bunch of dynamic leaves. Most simulations have tons of static or inactive objects. The benchmarks show that the new tree doesn't do a bad job on these by any means, but imagine all the leaves were static meshes. There's no point in being aggressive with refinements or cache optimizations because nothing is moving or changing, and there's no need for any collision self testing if static-static collisions don't matter.
This is important because the number of static objects can be vastly larger than the number of dynamic objects. A scene big enough to have 5000 active dynamic objects might have hundreds of thousands of static/inactive objects. The old broad phase would just choke and die completely, requiring extra work to use a StaticGroup or something (which still wouldn't provide optimal performance for statics, and does nothing for inactive dynamics). In contrast, a new broad phase that has a dedicated static/inactive tree could very likely handle it with very little overhead.
When I have mentioned big planned broad phase speedups in the past ("over 10 times on some scenes"), this is primarily what I was referring to. The 4 times speedup of the core rewrite was just gravy.
Now what?
If you're feeling adventurous, you can grab the tree inside of the new scratchpad repository on github. Beware, it's extremely messy and not really packaged in any way. There are thousands of lines of dead code and diagnostics, a few dependencies are directly referenced .dlls rather than nice nuget packages, and there's no documentation. The project also contains some of the vectorized trees (with far fewer features) and some early vectorized solver prototyping. Everything but the Trees/SingleArray tree variant is fairly useless, but it might be interesting to someone.
In the future, the scratchpad repo will be where I dump incomplete code scribblings, mostly related to BEPUphysics.
I'm switching developmental gears to some graphics stuff that will use the new tree. It will likely get cleaned up over time and turned into a more usable form over the next few months. A proper BEPUphysics v2.0.0 repository will probably get created sometime in H1 2016, though it will remain incomplete for a while after that.
